2015年北京数学文科试题及答案word在线版[二]
2015年北京文科数学填空题
(共6小题,每小题5分,共30分)
(9)复数i(1+i)的实数为
(10)2-3,3 ,log25三个数中最大数的是
,log25三个数中最大数的是
(11)在△ABC中,a=3,b=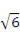 ,
,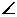 A=
A=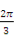 ,
,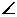 B=
B=
(12)已知(2,0)是双曲线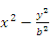 =1(b>0)的一个焦点,则b=.
=1(b>0)的一个焦点,则b=.
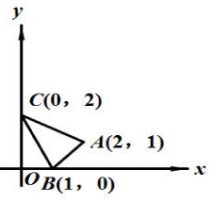
(13)如图,△ABC及其内部的点组成的集合记为D,P(x,y)为D中任意一点,则z=2x+3y的最大值为
(14)高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级中的排名情况如下,甲、乙、丙为该班三位学生。
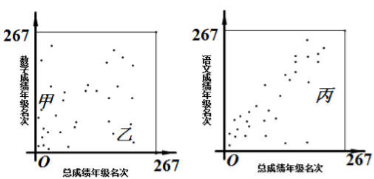
从这次考试成绩看,
①甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是
②在语文和数学两个科目中,两同学的成绩名次更靠前的科目是
2015年北京文科数学解答题
(共6题,共80分,解答应写出文字说明,演算步骤或证明过程。www.sczsxx.com)
(15)(本小题13分)
已知函数f(x)=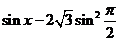
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)在区间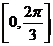 上的最小值。
上的最小值。
(16)(本小题13分)
已知等差数列{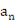 }满足
}满足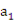 +
+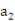 =10,
=10,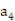 -
-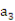 =2.
=2.
(Ⅰ)求{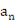 }的通项公式;
}的通项公式;
(Ⅱ)设等比数列{ }满足
}满足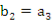 ,
,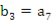 ;问:
;问: 与数列{
与数列{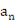 }的第几项相等?
}的第几项相等?
(17)(本小题13分)
某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成下统计表,其中“√”表示购买,“×”表示未购买。
| 商品
顾客人数 | 甲 | 乙 | 丙 | 丁 |
| 100 | √ | × | √ | √ |
| 217 | × | √ | × | √ |
| 200 | √ | √ | √ | × |
| 300 | √ | × | √ | × |
| 85 | √ | × | × | × |
| 98 | × | √ | × | × |
(Ⅰ)估计顾客同时购买乙和丙的概率
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
(18)(本小题14分)
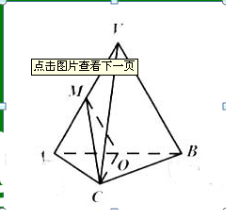
如图,在三棱锥E-ABC中,平面EAB ⊥平面ABC,三角形EAB为等边三角形,AC⊥ BC,且AC=BC=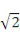 ,O,M分别为AB,EA的中点。
,O,M分别为AB,EA的中点。
(1) 求证:EB//平面MOC.
(2) 求证:平面MOC⊥平面 EAB
(3) 求三棱锥E-ABC的体积。
(19)(本小题13分)
设函数f(x)=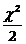
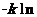 ,k>0
,k>0
(I)求f(x)的单调区间和极值;
(II)证明:若f(x)存在零点,则f(x)在区间(1,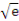 )上仅有一个零点。
)上仅有一个零点。
(20)(本小题14分)
已知椭圆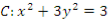 ,过点
,过点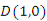 且不过点
且不过点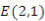 的直线与椭圆
的直线与椭圆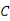 交于
交于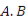 两点,直线
两点,直线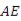 与直线
与直线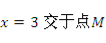 .
.
(1)求椭圆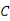 的离心率;
的离心率;
(II)若AB垂直于x轴,求直线BM的斜率;
(III)试判断直线BM与直线DE的位置关系,并说明理由。
(文章来源招生考试网,转载请注明原文出处: https://www.sczsxx.com/html/gaokaoziyuan/liniangaokaoshiti/2015/0609/119510.html)
- 热门内容



